Use group theory to obtain a qualitative MO energy level diagram for BCl3.
Which boron orbitals may be used in bonding.
iii) Select an appropriate basis to obtain a reducible representation. Reducing this will give irreducible representations (i.e. symmetries) for the orbitals in the basis.
For simplicity, assume that bonding involves the 2s and 2p orbitals on boron and the 3p orbitals on chlorine.
Use one 3p orbital on each chlorine pointing directly at boron (we'll call this pσ, see diagram) as a basis for a representation of the chlorine bonding orbitals. Linear combinations with appropriate symmetry can be combined with the boron atomic orbitals.
|
Click for larger image | 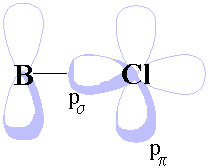
|
Constructing the molecular orbital diagram - All the required information has been determined above.
Comments:
|
The boron atom has an empty 2p orbital (symmetry a2″) perpendicular to the plane of the molecule that is available for π-bonding with some of the chlorine 3p orbitals. Use a pπ orbital (see diagram) on each chlorine atom as a basis to generate a new representation, and hence produce a new MO energy level diagram including the effects of π-bonding.
|
Click for larger image | 
|
Constructing the molecular orbital diagram - All the required information has been determined above.
Comments:
|
| Previous (Exercise 4) | Return to top of page | Next (Exercise 6) |