Molecular Symmetry and Group Theory

Workshop 5 — Chemical bonding

  • Return To Workshop Five Contents Page

    • Exercise 1

      Use the 4 C—H bonds in the CH4 molecule as a basis to obtain a representation in the tetrahedral point group Td, and reduce this to its component irreducible representations.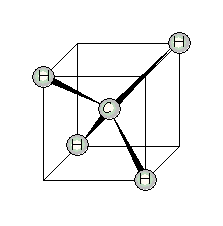

    Td E 8C3 3C2 6S4 6σd
    Γ 4


    Click for larger image

    Td E 8C3 3C2 6S4 6σd
    Order =
    		 
    Γ 4    
    A1 1 1 1 1 1
    A2 1 1 1 -1 -1
    E 2 -1 2 0 0
    T1 3 0 -1 1 -1
    T2 3 0 -1 -1 1
    N×χR×χI(A1)
    Σ(N×χR×χI(A1)) =
    Σ(N×χR×χI(A1))/Order =
    N×χR×χI(A2)
    Σ(N×χR×χI(A2)) =
    Σ(N×χR×χI(A2))/Order =
    N×χR×χI(E)
    Σ(N×χR×χI(E)) =
    Σ(N×χR×χI(E))/Order =
    N×χR×χI(T1)
    Σ(N×χR×χI(T1)) =
    Σ(N×χR×χI(T1))/Order =
    N×χR×χI(T2)
    Σ(N×χR×χI(T2)) =
    Σ(N×χR×χI(T2))/Order =

    Therefore, the composition of Γ is:   Γ = A1 + A2 + E + T1 + T2

    Td E 8C3 3C2 6S4 6σd    
    A1 1 1 1 1 1   x2+y2+z2
    A2 1 1 1 -1 -1    
    E 2 -1 2 0 0   (2z2-x2-y2,x2-y2)
    T1 3 0 -1 1 -1 (Rx,Ry,Rz)  
    T2 3 0 -1 -1 1 (x,y,z) (xy,xz,yz)

      Which C valence orbitals correspond to these irreducible representations?  
    Comments:
    		 
       

    Workshop Contents Return to top of page Next (Exercise 2)