|
Molecular Symmetry and Group Theory |
Group theory is very important in the interpretation of the vibrational properties of molecular species, which can be investigated by infra-red (IR) or Raman spectroscopy. Whereas IR spectroscopy probes the molecular vibrations directly by measuring the absorption of infra-red radiation, Raman spectroscopy examines the change in energy of higher energy photons scattered through their interaction with the vibrations.
Although similar information is obtained from these two spectroscopic methods, the selection rules are different:
Group theory enables us to determine the symmetries of molecular vibrations and to establish whether the vibrations are IR or Raman active (Exercise 1&2).
In order to perform a full analysis of the vibrational modes of a molecule we need to consider in detail the motion of every atom. Three arrows (along the x, y and z directions) on each atom therefore provide the appropriate basis for our treatment. We must remember, however, that some of the atomic movements correspond not to vibrations, but to rotations or translation of the whole molecule. These translational and rotational modes need to be removed in order to obtain the symmetries of the vibrational modes.
The procedure can be summarized as follows:
IR — for a vibration to be IR active the irreducible representation must be appropriate to cause a change in the dipole moment of the molecule. This is a directional property and any vibration with an irreducible representation corresponding to the x, y or z directions as indicated in the character table will be IR active.
Raman — for a vibration to be Raman active the irreducible representation must be appropriate to cause a change in the polarizability of the molecule. This is true when the irreducible representation corresponds to terms such as x2, y2, z2, xy, yz, xz, or linear combinations of these (e.g. x2-y2) in the character table.
Rotation of cartesian axes
If an axis is rotated through angle θ it contributes cos θ to the character of the Cartesian representation. Therefore,
| Operations | E | σ | i | C2 | C3 | C4 | C5 | C6 | S3 | S4 | S5 | S6 | S8 |
| f(R) | 3 | 1 | -3 | -1 | 0 | 1 | 1.618 | 2 | -2 | -1 | 0.382 | 0 | 0.414 |
For any Cn , f(R) = 1 + 2cos(2π/n)
For any Sn , f(R) = -1 + 2cos(2π/n)
Molecules containing groups with characteristic stretching vibrations
IR and Raman measurements show that the frequencies of CO stretching vibrations of transition metal complexes typically fall in the range 1700-2000 cm-1. If we are interested in these characteristic vibrations we can select a basis that gives us only the irreducible representations relating to these stretches.
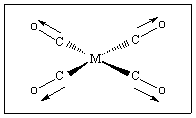
| For example, for the square planar carbonyl complex shown, we can take the four arrows shown to represent the CO stretching vibrations, and use these as our basis. | 
|
| In this case, the basis chosen does not include translational or rotational motion of the molecule, and all the irreducible representations correspond to CO stretching vibrations. The identification of IR and Raman active vibrations proceeds in the same way as for the full vibrational analysis (Exercise 3). |