|
Molecular Symmetry and Group Theory
Lecture 4 — Matrices and degenerate representations
|
Lecture Summary
If a molecule has a proper rotation axis of order 3 or more, the application of some symmetry operations inevitably causes certain directional properties to be interconverted.
|
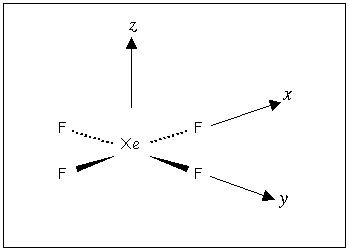
| For example, the application of the C4 operation on the square planar molecule XeF4 [Point group?] converts a Xe px orbital into py, and py into -px. For the C4 operation to be valid the px and py orbitals must be identical and have the same energy i.e. they must be degenerate.
As the effect of the C4 operation on the px and py orbitals is not, for example, a simple inversion, it is impossible to describe by a single number. In this situation the px and py orbitals cannot be treated separately, but must be considered as a pair. Together these orbitals belong to a degenerate representation.
| 
|
If two directional properties are mixed by a symmetry operation, the effect of the operation can only be described by an array of numbers known as a matrix.
|
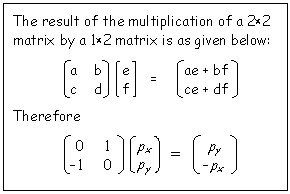
| Following the rules of matrix multiplication (see inset), the effect of the matrix 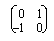 operating on the px and py orbitals is to convert px to py and py to -px: exactly the result of the C4 operation. Thus the matrix given describes the effect of the C4 operation. operating on the px and py orbitals is to convert px to py and py to -px: exactly the result of the C4 operation. Thus the matrix given describes the effect of the C4 operation.
| 
|
The sum of the elements on the leading diagonal (top left to bottom right i.e. a + d in the example above) of a square matrix is known as the character (or trace) of the matrix. It is this number that appears in character tables.
Note that the character is all that we need to apply group theory: we do not need the actual matrix.
The character of the matrix tells us to the extent to which the objects operated on (in this case the px and py orbitals) are ‘converted into themselves’ by the operation. As px is transformed into py, and py into -px, in this case the character is zero.
By convention doubly degenerate representations are labelled E and triply degenerate representations are labelled T.
In the point group D4h, the px and py orbitals transform according to the representation labelled Eu. The subscript ‘u’ (for ungerade) indicates that it is anti-symmetric with respect to the inversion operation i.
The subscript ‘g’ (gerade) is used for representations that are symmetric to inversion.
The full set of symmetry operations for D4h, and the characters of the Eu irreducible representation, are as follows:
| D4h | E | 2C4 | C2 | 2C2′ | 2C2″ | i | 2S4 | σh | 2σv | 2σd |
| | Eu | 2 | 0 | -2 | 0 | 0 | -2 | 0 | 2 | 0 | 0 | (x,y)
| |
Note that in character tables, degenerate directional properties (e.g. x and y) are bracketed together. This enables us to tell that certain orbitals such as px and py are degenerate. [Similarly in the D4h point group, dxz and dyz are also degenerate.]
The characters in the table relate very simply to the extent to which the px and py orbitals are converted into themselves. Thus for C4 (px → py, py → -px) the character is zero, but for C2 about the same axis (px → -px, py → -px) the character is -2.
|
| So far we have considered the effects of the C4 operation on only the Xe px and py orbitals. These orbitals are said to provide a basis for obtaining a representation of the C4 operation.
In general, a wide variety of different bases may be chosen depending on the nature of the problem being considered.
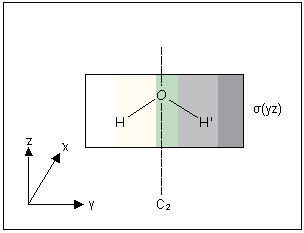
For example, we may use the two O—H bonds in H2O as a basis for the C2 operation of C2v. As C2 converts O—H to O—H′ and vice versa, neither bond is converted into itself to any extent, and so the character of the matrix that describes this transformation must be zero.
| 
|
The σ(yz) operation, however, leaves both bonds unmoved, so its character must be 2.
[Similarly the character of the matrices describing E and σ(xz) are 2 and 0 respectively]

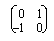 operating on the px and py orbitals is to convert px to py and py to -px: exactly the result of the C4 operation. Thus the matrix given describes the effect of the C4 operation.
operating on the px and py orbitals is to convert px to py and py to -px: exactly the result of the C4 operation. Thus the matrix given describes the effect of the C4 operation.

